题目：

一个山头呼喊的声音可以被临近的山头同时听到。题目假设每个山头最多有两个能听到它的临近山头。给定任意一个发出原始信号的山头，本题请你找出这个信号最远能传达到的地方。

输入格式：

输入第一行给出3个正整数n、m和k，其中n（$\le$10000）是总的山头数（于是假设每个山头从1到n编号）。接下来的m行，每行给出2个不超过n的正整数，数字间用空格分开，分别代表可以听到彼此的两个山头的编号。这里保证每一对山头只被输入一次，不会有重复的关系输入。最后一行给出k（$\le$10）个不超过n的正整数，数字间用空格分开，代表需要查询的山头的编号。

输出格式：

依次对于输入中的每个被查询的山头，在一行中输出其发出的呼喊能够连锁传达到的最远的那个山头。注意：被输出的首先必须是被查询的个山头能连锁传到的。若这样的山头不只一个，则输出编号最小的那个。若此山头的呼喊无法传到任何其他山头，则输出0。

输入样例：

7 5 4
1 2
2 3
3 1
4 5
5 6
1 4 5 7

输出样例：

2
6
4
0

思路：

其实本题的解法有很多，可以用BFS（宽度搜索）一层一层地看。

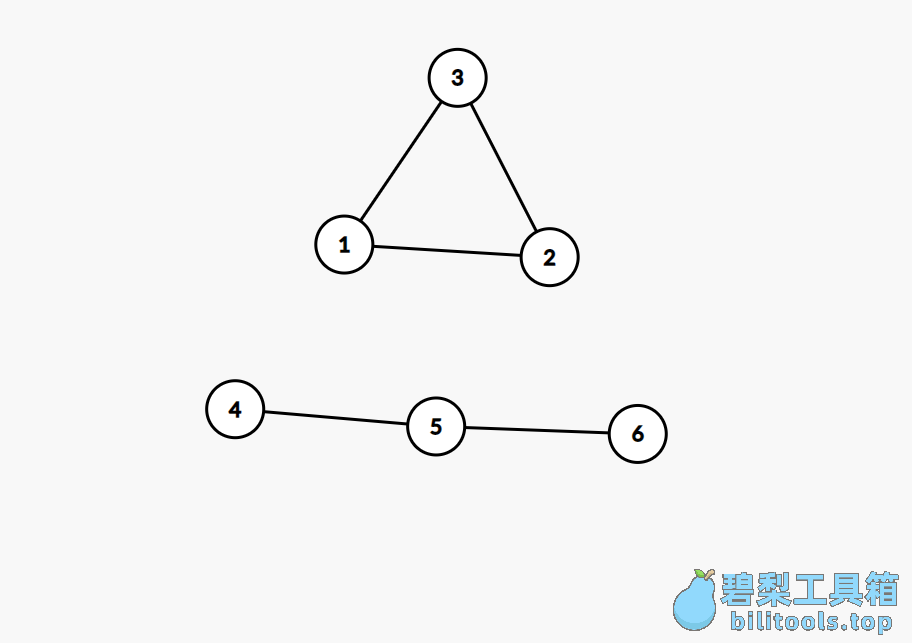
例如，上面输入样例，可以画为：

（这里推荐一个在线画图网站：https://csacademy.com/app/graph_editor/）

例如，当搜索节点1时：

会搜索2和3两个节点。但是题目要求，当距离一样时，输出标号最小的那个：

若这样的山头不只一个，则输出编号最小的那个

我认为这里可以有两种方法：

• 搜索同一层时，记录标号最小的那个：可以记一个变量，利用min()函数维护这个变量。
• 读入数据后，先将每一个节点的子节点分别按照从大到小的顺序排列，这样BFS按顺序处理后，同一层中最后一个节点就是我们想要的。

下面的代码中我用的是上面第二种方法。

其他的就是BFS的套路了，没啥可说的，都写注释了。

解法：

#include <bits/stdc++.h>
using namespace std;

const int N = 10010;
vector<int> G[N]; // 记录每个节点的子节点
int vd[N]; // "visited"的缩写，标记是否被搜索过，默认0未搜索，搜索过记为1
int n;

int bfs(int u)
{
    if (G[u].empty()) {
        // 如果当前节点没有子节点，按照题意返回0
        return 0;
    }

    memset(vd, 0, sizeof(vd)); // 一些节点在其他节点可能被搜索过，但是管我这一轮搜索什么事，全部重置状态为未搜索过
    queue<int> q;
    q.push(u);
    int last; // 记录最后访问的节点，当这一轮循环结束后留下的即为最远层的编号最小的节点
    while (!q.empty()) {
        int tmp = q.front();
        vd[tmp] = 1;
        for (int v : G[tmp]) {
            if (!vd[v]) {
                q.push(v);
                last = v;
                vd[v] = 1;
            }
        }
        q.pop();
    }
    return last;
}

int main()
{
    int m, k;
    cin >> n >> m >> k;
    // 读入数据，建立各个节点的对应关系
    while (m--) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }

    // 将每个节点的子节点按照从大到小排序
    for (int i = 1; i <= n; i++) {
        sort(G[i].begin(), G[i].end(), greater<int>());
    }

    while (k--) {
        int a;
        cin >> a;
        cout << bfs(a) << endl;
    }

    return 0;
}